| Inicio » Archivos » Juegos y Actividad Física » Juegos de Pensar |
Juegos para Pensar
DINÁMICA DE GRUPOS JUEGOS DE INGENIO - JUEGOS PARA PENSAR ■ 1. El cuadrado mágico Sobre un cuadrado de 9 casillas, deben colocarse nueve números distintos: los comprendidos entre el 1 y el 9, ambos inclusive; por tanto, se trata de no repetir ninguno. Una vez dispuestos, la suma de las columnas horizontales, verticales y diagonales ha de dar siempre el mismo resultado.
■ 2. El testamento del jeque Según su última voluntad, los camellos del jeque deben repartirse entre sus hijos de la siguiente manera: la mitad para el primogénito, una cuarta parte para el segundo y una sexta para el menor. Pero el hecho es que el legado constaba de 11 camellos y los hermanos no se ponían de acuerdo en la forma de repartirlos. Decidieron finalmente consultar a un viejo beduino famoso por su sabiduría, y éste les ofreció su propio camello para que se completase la docena. Como los jóvenes se negaron en principio a aceptarlo, el beduino los tranquilizó afirmando: - No os preocupéis, que yo nada he de perder con esto. Hecha la operación, resultó efectivamente así. ¿Cómo es posible?
■ 3. En su precio justo Una botella y su tapón valen en conjunto 1,10 euros. La botella cuesta 1 euro más que el tapón. ¿Cuánto vale la botella? ¿Y el tapón?
■ 4. Blanco, rubio y castaño Tres personas apellidadas Blanco, Rubio y Castaño se conocen en una reunión. Poco después de hacerse las presentaciones, la dama hace notar:
- Es muy curioso que nuestros apellidos sean Blanco, Rubio y Castaño, y que nos hayamos reunido aquí 3 personas con ese color de cabello. - Sí que lo es -dijo la persona que tenía el pelo rubio-, pero habrá observado que nadie tiene el color de pelo que corresponde a su apellido. - ¡Es verdad! -exclamó quien se apellidaba Blanco. Si la dama no tiene el pelo castaño, ¿de qué color es el pelo de Rubio?
■ 5. La astucia del príncipe extraviado Las tradiciones aseveran que -en el reino de lo imaginario- existen 2 regiones llamadas respectivamente Sincerio y Falsio. Como puede desprenderse de sus nombres, lo que las caracteriza es la actitud de sus habitantes ante la verdad. Un príncipe que se hallaba extraviado por esas tierras deseaba saber si estaba en Sincerio o en Falsio. Se acercó a un morador de una cabaña y le hizo una pregunta: ¿es usted natural de este país? De la respuesta afirmativa supo donde se hallaba y enderezó su senda. ¿Dónde se hallaba y cómo llegó a dicha conclusión?
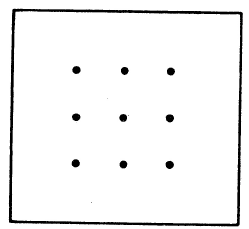
■ 6. Unir nueve puntos Se trata de unir estos 9 puntos mediante 4 trazos rectilíneos continuos. Es decir, sin levantar el lápiz del papel, ni recorrer 2 veces el mismo trazo.
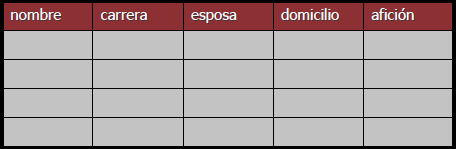
■ 7. La composición de las familias Los cuatrillizos que viven en A ya han cumplido 40 años. Todos ellos están casados, y tienen resuelta su vida vocacional y afectiva. En el cuadro inferior habrá que ubicar a los personajes, su domicilio, etc., tomando en cuenta las pistas que se dan a continuación: - El ingeniero no se casó con Elisa, pero es un enamorado de la pesca. - El que vive en C se casó con Juana y no es precisamente Alfredo. - Patricia conoció a su marido cuando éste estudiaba la carrera de física. - El aficionado a la música se quedó a vivir en A, y el abogado se fue a B. - Manolo no comparte la afición al fútbol de su hermano. El que se casó con María no es militar. En D no viven ni Juan ni Ricardo, aunque si vive el aficionado a la pesca. - A Elisa, igual que a su cuñada, le gusta la electrónica. El aficionado al fútbol es Alfredo, y el que vive en C es Ricardo. ¿Quién se gasta todo el dinero en discos?
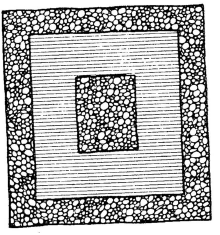
■ 8. Cruzar el foso El dibujo representa 1 plataforma interior rodeada por un foso de 3m de ancho, lleno de agua. Se trata de llegar a la plataforma sin mojarse, pero para ello no se dispone más que de 2 tablones de madera de exactamente 3m cada uno, lo que hace que ninguno de ellos tenga el largo suficiente como para poyarse en ambas orillas. ¿Cómo hacer para llegar a la plataforma interior?
■ 9. Conjunto geométrico Formar un conjunto geométrico que contenga 2 cuadrados y 4 triángulos, empleando para ello sólo 8 palillos.
■ 10. Sencillo pero difícil Con sólo 5 palillos deben poder construirse 2 triángulos equiláteros.
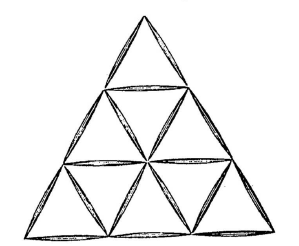
■ 11. Eliminando triángulos Con 18 palillos se obtiene el triángulo que aparece al principio de la página siguiente, compuesto por otros 9 triángulos más pequeños. Retirando sólo 6 palillos, esos 9 triángulos deben quedar convertidos en 4.
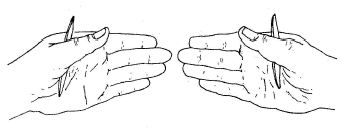
■ 12. Cambio de mano Se toma 1 palillo en cada mano, y se coloca entre el dedo pulgar y la palma. Cada mano, mediante sus dedos pulgar y medio y al unísono, debe tomar y retirar el palillo de la mano contraria, sin que ambas manos queden en ningún momento entrelazadas.
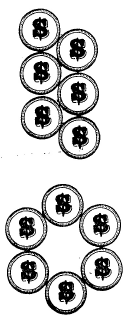
■ 13. Cambio de figura Se colocan 6 monedas de la forma que puede verse en el diagrama superior. Con sólo 3 movimientos, la figura quedará convertida en 1 circunferencia, tal como se ve en la otra ilustración. Las reglas del juego son simples pero estrictas: tienen que efectuarse 3 movimientos, ni más ni menos; en cada movimiento sólo puede desplazarse una moneda; al llegar a su nueva posición, la moneda desplazada deberá quedar en contacto con otras dos monedas.
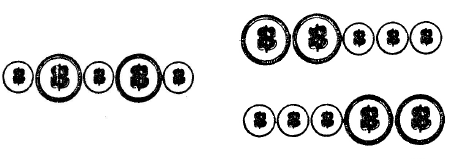
■ 14. Paso de monedas 3 monedas pequeñas y 2 grandes se disponen sobre una mesa tal como aparece en la figura. Con los dedos índice y medio de una misma mano, deben tomarse a un tiempo una moneda grande y una pequeña, cambiándolas de posición. La única regla consiste en que las 2 monedas se desplacen en cada movimiento deberán ser siempre una grande y una pequeña, y siempre también tendrán que estar contiguas (o sea, una al lado de la otra). Por lo demás, las combinaciones y variantes son libres.
El objetivo del juego es dejar todas las monedas pequeñas juntas, seguidas de las grandes, o viceversa. El juego concluye, por tanto, al alcanzar una de estas dos posiciones.
■ 15. Desaparición de una moneda Tres amigos toman café en la terraza de 1 bar, y el camarero les cobra por ello 7,50 euros. Cada uno paga sus correspondientes 2,50, pero hacen saber que el precio les parece abusivo. Enterado el dueño de la queja, dice al camarero que les devuelva 2,50, pero éste considera que se trata de una cifra no divisible por 3, así que lo soluciona a su manera: devuelve 0,50 a cada uno de los clientes y se queda con 1 euro. Entonces aparece el problema: los amigos pagaron 2 euros cada uno (2,50-0,50), lo que hace un total de 6 euros, a lo que hay que sumar 1 que se quedó el camarero. El resultado es 7; por lo que, extrañamente, ha desaparecido una moneda de 0,50. ¿Cuál es la solución?
■ 16. Anudados Para este juego son necesarias 2 personas y 2 cuerdas. Se ata un extremo de la primera cuerda a la muñeca derecha de una persona, y el otro extremo a su muñeca izquierda. La segunda cuerda se pasa entre el cuerpo de esta persona y la cuerda que une sus muñecas: sólo entonces los extremos de esta segunda cuerda se atan a las muñecas de otra persona. Las 2 personas han quedado atadas una a la otra, ¿cómo lograrán desatarse, sin desatar previamente por lo menos una de sus muñecas?
| |
| Categoría: Juegos y Actividad Física, Juegos de Pensar |
|
|
| ¡No dudes en dejar un comentario! | |